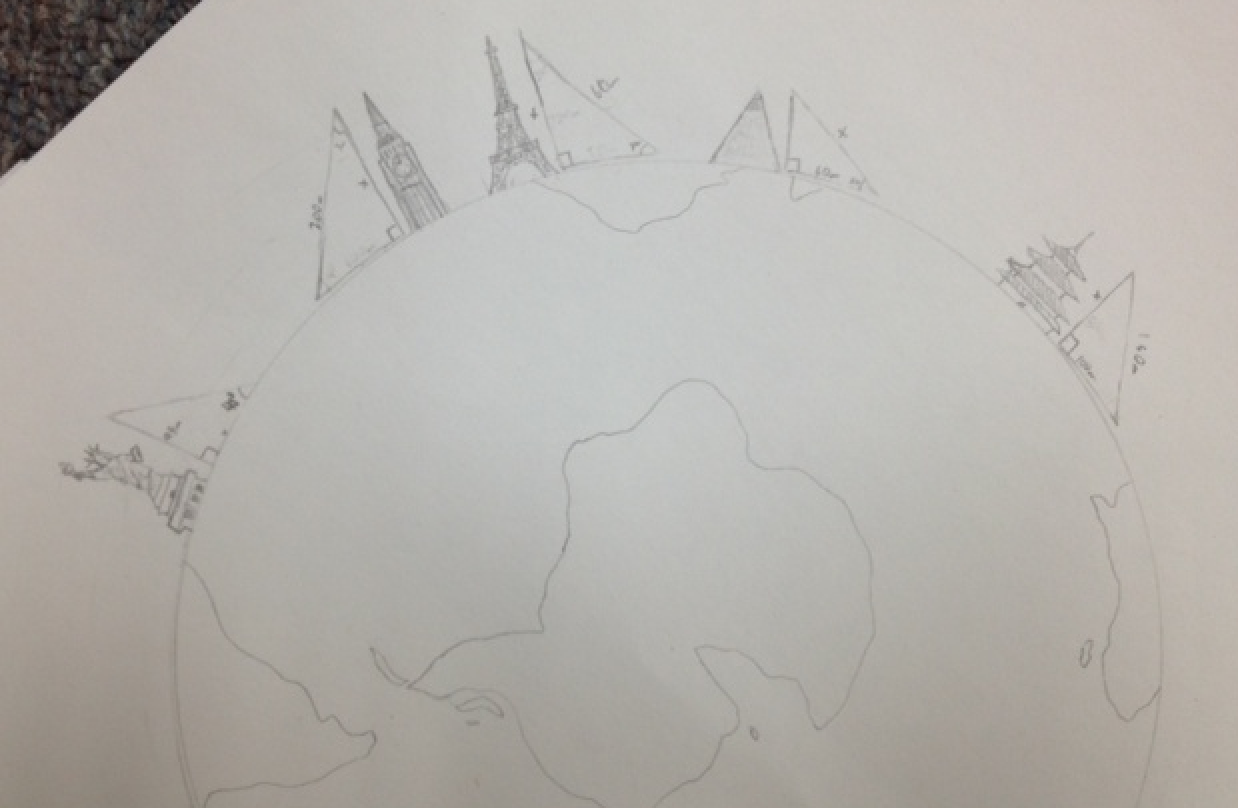
So, as I mentioned in a previous post, I've had my students build their own trig-tables this year and I must say that they are doing extremely well! I was inspired by my amazing colleague, Amy Zimmer (http://zicker63.blogspot.com) to do this fun activity with my students. The original document involved a scene set in a park (see below, original document found at: http://www.funmaths.com/worksheets/downloads/view.htm?ws0012_1.gif) and Amy thought that it would be cool to switch it up and have the students come up with their own scene. In the woods, at the beach, in the kitchen, etc.
The requirement for the assignment was that they needed to create some sort of scene or scenario where they were setting up right triangles that they could solve for missing sides and angles. Another requirement was that they needed to set up one problem that involved using the ratio altitude/base, one using altitude/hypotenuse, and one using base/hypotenuse, all given one acute angle and one of the side lengths in the ratio. The fourth type of triangle they had to set up should have had both acute angles missing and given two side lengths, basically using inverse trig. The fifth triangle did not have a requirement, they could repeat any of the other types of triangles (the wildcard).
I enjoyed seeing their work and seeing how creative they got. The creation of the poster was essentially phase one of the activity and phase two was actually solving for all missing values of the triangle. Students jumped right in to using their trig charts and did surprisingly well with the triangles that were missing their acute angles. I really enjoyed seeing them do this because I think even high school students need to show their inner artist and get a little crafty sometimes. I had them staple their work to the back of the poster and any student that worked on the poster had to submit a page of work. I've included some of my favorites. Thanks, Amy for the inspiration! Enjoy!
From Amy Zimmer's Class:
Tuesday, April 15, 2014
Tuesday, April 8, 2014
Building Trig Tables
I'm sure I'm not the only Geometry teacher out there who gets frustrated with how their textbook approaches a subject. Right Triangle Trigonometry, for me, is one of those subjects. The textbook that my school uses just dives right in to introducing sine, cosine, and tangent with little to no context, and certainly no mention of similar right triangles. So, this year, I decided to do things a little differently.
A few months ago I was doing some work with the incredible Kate Nowak and this exact topic came up. She shared with us that when she was a classroom teacher, she had her students build their own trig tables and she ended the lesson with a Romeo & Juliet problem where Romeo needed to find how high the balcony was so that he could climb to see his star-crossed lover. (Check out Kate's blog post: http://function-of-time.blogspot.com/2009/04/introducing-right-triangle-trig.html) I thought I would give it a shot with my students.
I am teaching 6 sections of Geometry this year, so I thought that this would be a great opportunity to collect lots of data to calculate some reasonable values for sine, cosine, and tangent, even though they would not be called that until later.
Much like Kate's blog suggests, I had my students start by drawing 5 right triangles with a specified acute angle on an 8.5 by 11 piece of printer paper. This was challenging for some because a lot of my students do not know how to operate a protractor. Once we got over that hurdle, they were on their way.
After drawing their 5 right triangles, I set them up to measure the three side lengths of each triangle, using Kate's handout, students recorded their measurements. The third step was to calculate the ratios of the side lengths (aka: sine, cosine, tangent) :) of their 5 triangles. Lightbulbs began to go on around the room because students were realizing that their ratios for the 5 different triangles were all the same (or at least pretty close). This was a great opportunity to take a look at some data and discuss potential outliers or mistakes. Here's a sample of student data:
What I found was that students were not yet ready to be the "critical consumers" that I was wanting them to be. This sample doesn't have any glaring errors, but nevertheless, they were willing to accept the data at face value. I asked them to look for patterns and initially I was hearing things like "It's going up by 0.3". Well, that may be true for the "altitude" column from row 1 to row 2, but they didn't know how to look for any other type of pattern. Finally someone said, "They're all increasing," which was wonderful to hear! We talked about why that was a good sign and why it made sense. Then another student pointed out that the hypotenuse values were always the largest in the set of 3 data points and we discussed why that was a good thing. Next, we practiced finding the ratios to make sure that they were dividing correctly. It was great to discuss why all the numbers should be less than 1 or why a number should be bigger than another; conversations that I don't think they had ever had. Lastly, we practiced finding the averages of the 5 different ratio entries. I have to say, this was a bit of a train wreck! For example, in the first column (a/b), students told me that the average was 1.4 or something like that. They didn't understand why that was not possible. After some discussion, they were convinced that the average needed to be closer to 0.2-something.
Because I have so many sections of Geometry and so many students in each section, I thought this would be a great opportunity to collect lots of data, but also calculate averages. Each student was working with a specific acute angle, but so was their partner, so once they got their ratio averages, I had them average their averages with their neighbor. That's what we wrote in the yellow charts on the board (see below).
The last step in this process was to look at all this data and determine if the numbers were reasonable from all 6 classes. I told the students that if they were comfortable with all the entries, they should calculate the average, if they felt that there was an outlier (or more than one), they should be able to defend why, throw it out, and then find the average of the remaining numbers. This was an interesting process because some students argued to keep specific numbers while others fought to get rid of them. The final product for each class was their own trig table (see below), which was a lot of work, but now we were ready to do some trig! :)
So, now it was time to actually do some work and I had a moment of panic (I actually lost some sleep over this) because I wasn't sure how I was going to bring this all together. Kate's worksheet had some great questions, so I started there. First of all, I wanted to take some time to marvel at the fact that all of this data collection happened independently (no two classes worked together), so how was it that their data was so close? To my surprise, it seemed that students had already considered this and very quickly responded with "Because the triangles are similar!" We discussed this further and it was clear that they understood the idea of similar triangles by AA. I felt they were ready to put this stuff to good use.
The last problem on Kate's handout involved Romeo & Juliet, and I thought we could give it a shot. I tried a sample using a 30 degree angle and a base of 50 feet. I asked students what I was solving for, they knew it was altitude, and then I asked, do I know anything about the relationship between altitude and base of a right triangle with a 30 degree angle? And that's when the lightbulbs REALLY started to go on! What an amazing moment for the students to realize that all of their hard work had lead them to this place where they could solve a problem without me telling them what to do. They were off to the races and solving for all different angles.
The last thing that I did was said, "Now, Romeo really wants to impress Juliet, so he is fashioning a zip-line for her to ride down and meet him. If he is 70 feet away, how long with the line need to be for your given angle?" Some started to set up the same ratio as before, but quickly realized that this relationship was now base and hypotenuse. After realizing that, they were able to set up the correct equation, but I have to say, solving it proved to be a bit more difficult. :)
Even though I spent a whole week doing this with my students (3 periods on block schedule), I feel that it was totally worth the time and effort that the students put in. They worked with data, they were critical, precise, and thoughtful, which are things that don't usually happen for them in a math classroom. Overall, I feel that this was a huge success, but I am already waiting for them to get mad at me when I tell them that they can just use a calculator to do some of this stuff. :)
A few months ago I was doing some work with the incredible Kate Nowak and this exact topic came up. She shared with us that when she was a classroom teacher, she had her students build their own trig tables and she ended the lesson with a Romeo & Juliet problem where Romeo needed to find how high the balcony was so that he could climb to see his star-crossed lover. (Check out Kate's blog post: http://function-of-time.blogspot.com/2009/04/introducing-right-triangle-trig.html) I thought I would give it a shot with my students.
I am teaching 6 sections of Geometry this year, so I thought that this would be a great opportunity to collect lots of data to calculate some reasonable values for sine, cosine, and tangent, even though they would not be called that until later.
Much like Kate's blog suggests, I had my students start by drawing 5 right triangles with a specified acute angle on an 8.5 by 11 piece of printer paper. This was challenging for some because a lot of my students do not know how to operate a protractor. Once we got over that hurdle, they were on their way.
After drawing their 5 right triangles, I set them up to measure the three side lengths of each triangle, using Kate's handout, students recorded their measurements. The third step was to calculate the ratios of the side lengths (aka: sine, cosine, tangent) :) of their 5 triangles. Lightbulbs began to go on around the room because students were realizing that their ratios for the 5 different triangles were all the same (or at least pretty close). This was a great opportunity to take a look at some data and discuss potential outliers or mistakes. Here's a sample of student data:
Because I have so many sections of Geometry and so many students in each section, I thought this would be a great opportunity to collect lots of data, but also calculate averages. Each student was working with a specific acute angle, but so was their partner, so once they got their ratio averages, I had them average their averages with their neighbor. That's what we wrote in the yellow charts on the board (see below).
Each class generated this chart and now it was time to compare the charts from the 6 different classes. I asked students to help me calculate averages from the yellow chart (if there was more than one entry) as well as help me understand if any of the numbers just did not make sense. They picked up on things like increasing and decreasing patterns, and if there were two entries in a cell they were able to compare two numbers and see if they were reasonable or not. The next step involved me writing up the numbers from each class into a fairly large chart on the white board (see below).
So, now it was time to actually do some work and I had a moment of panic (I actually lost some sleep over this) because I wasn't sure how I was going to bring this all together. Kate's worksheet had some great questions, so I started there. First of all, I wanted to take some time to marvel at the fact that all of this data collection happened independently (no two classes worked together), so how was it that their data was so close? To my surprise, it seemed that students had already considered this and very quickly responded with "Because the triangles are similar!" We discussed this further and it was clear that they understood the idea of similar triangles by AA. I felt they were ready to put this stuff to good use.
The last problem on Kate's handout involved Romeo & Juliet, and I thought we could give it a shot. I tried a sample using a 30 degree angle and a base of 50 feet. I asked students what I was solving for, they knew it was altitude, and then I asked, do I know anything about the relationship between altitude and base of a right triangle with a 30 degree angle? And that's when the lightbulbs REALLY started to go on! What an amazing moment for the students to realize that all of their hard work had lead them to this place where they could solve a problem without me telling them what to do. They were off to the races and solving for all different angles.
The last thing that I did was said, "Now, Romeo really wants to impress Juliet, so he is fashioning a zip-line for her to ride down and meet him. If he is 70 feet away, how long with the line need to be for your given angle?" Some started to set up the same ratio as before, but quickly realized that this relationship was now base and hypotenuse. After realizing that, they were able to set up the correct equation, but I have to say, solving it proved to be a bit more difficult. :)
Even though I spent a whole week doing this with my students (3 periods on block schedule), I feel that it was totally worth the time and effort that the students put in. They worked with data, they were critical, precise, and thoughtful, which are things that don't usually happen for them in a math classroom. Overall, I feel that this was a huge success, but I am already waiting for them to get mad at me when I tell them that they can just use a calculator to do some of this stuff. :)
Thursday, March 27, 2014
Mathematical Modeling: Best Night's Sleep
I got a Jawbone band for Christmas this year and I have loved seeing how well I do in achieving my sleep goal and steps goal. I am finding that I am actually a really good sleeper and that my attempt to take 10,000 steps a day is hit or miss. As a teacher, I do better with my steps on the weekend and days when my students are testing are my worst. I thought that my students could benefit from taking a look at some real-life data and apply what they've learned from our studies of ratio, similarity, and proportions.
With almost 200 students this year, I did not want to grade that many tests for the end of the chapter, so I made this a group assessment. My students sit in groups of four as it is, so the groups were already chosen. As you can see from the write-up below, each student had a different responsibility in the group. Students dove in to the data before choosing roles that spoke to them. I was impressed to see how many different methods there were that students latched on to. Some chose percentages, some chose to represent their data in bar graphs, other pie charts; it was interesting to see what they were drawn to.
Here are the three pieces of data that I showed the students:
I found that students really struggled to understand how they could translate this data into a common measurement. Lots of students used percent, which I thought was great, but if they didn't think to use percentage, they struggled to come up with an alternate way.
I have to say that I was please with the level of engagement and focus that my students exhibited. They were interested to know who got the most sleep and what the data meant. I felt that this was a good exercise in mathematical modeling because students did not feel the pressure of arriving at the "right" answer and they were rewarded for their process as opposed to their answer. Also, the use of real-world data was beneficial and useful because it made things more applicable and gave the activity context...everybody has slept before. :)
With almost 200 students this year, I did not want to grade that many tests for the end of the chapter, so I made this a group assessment. My students sit in groups of four as it is, so the groups were already chosen. As you can see from the write-up below, each student had a different responsibility in the group. Students dove in to the data before choosing roles that spoke to them. I was impressed to see how many different methods there were that students latched on to. Some chose percentages, some chose to represent their data in bar graphs, other pie charts; it was interesting to see what they were drawn to.
Here are the three pieces of data that I showed the students:
I actually cut off the bottom portions that showed the amount of sound sleep, deep sleep, how long it took to fall asleep, and how long each person was in bed for. Students were given the bar graphs as well as the amount of time each person slept and what percent of their goal was met.
I started class by showing the three graphs through the projector so that they could see them with color. Students determined what the data showed them, what additional information they needed to know, and asked other questions that came up. I chose to answer some and leave some for them to answer because the data was available to do so.
At this time, I gave students the following handout for them to read and decide what role they were interested in.
__________________________________________________________________________________________________________________________________________________________________
Name:
____________________________________________
Geometry 2013-2014
Date:
_____________________________ Block: ________
Chapter 7 Similarity Test: Who Got the Best Night's Sleep?
This is a group test, but each student is responsible for submitting
his or her own portion of the test. Please
put a check next to the role that you had in your group in the list below. If you are a group of 4, each student should
take on one role. If you are a group of
3, each student will take on their own role and then share the role of
“Processor”. When your group is
finished, please staple all of the parts together with this page as a “cover
page” for each section. Please staple
the pages in the order as they appear below.
________
Group Member 1: Graphics
When considering who got the best
night's sleep, it’s important to compare “apples to apples”. You may notice that in the three sets of data
that I provided you, all three of them use different scales because they went
to bed and woke up at different times.
The job of the Graphic team member is to create a visual that uses the
same scale for all three sets of data and create this graphic in a way that
helps support your argument for who got the best night sleep. You will be graded on accuracy, neatness, and
quality of your graphic.
________
Group Member 2: Data
Looking at the three sets of data,
you can see that there is some “number crunching” to do. In order to compare the three sets of data
accurately, you need to use the same scale or the same units of measure. It is your responsibility to help your group
make sense of the numbers so that you can compare them accurately. You will be graded on the accuracy, neatness
and quality of your calculations.
________
Group Member 3: Argument Writer
I purposefully chose data that
didn’t have a “clear winner” so that you would have to defend your answer to
“Who got the best night's sleep?” Think
about what you value in a “good” sleep.
Is it length of time spent sleeping?
Most deep sleep? There is no
right answer here, so you need to convince me that your answer is correct. Imagine that you are convincing a skeptic, or
someone who got a different answer than you.
You will be graded on the clarity of your argument, how well you connect
it to your data and graphic, and the quality of your writing.
________
Group Member 4: Processor
I may have some questions as to how
you arrived at your final answer, but that’s why we have the Processor. I would like to know how your group worked
together to come to your final answer.
This should be a descriptive account of what your group did, but more
importantly, WHY? Because this is a
chapter test on similarity, please make sure to mention HOW you used
similarity, ratios, and/or proportions.
You will be graded on the clarity of your process description, how well
you connect it to the other three group members, and the quality of your
writing.
_________________________________________________________________________________
_________________________________________________________________________________
I have to say that I was please with the level of engagement and focus that my students exhibited. They were interested to know who got the most sleep and what the data meant. I felt that this was a good exercise in mathematical modeling because students did not feel the pressure of arriving at the "right" answer and they were rewarded for their process as opposed to their answer. Also, the use of real-world data was beneficial and useful because it made things more applicable and gave the activity context...everybody has slept before. :)
Monday, March 3, 2014
Transitioning to Transformations
Last week I gave my students a task from Illustrative Mathematics called Similar Triangles as an introduction to the concept of Angle-Angle Similarity. Here's how it played out...
A brief disclaimer is that although I have been teaching Geometry all year, I have not made the complete transition to teaching it through Transformations. I have done a few things here and there, but more than anything it was to try tasks and strategies out for myself and to challenge my students. They have had some experience with transformations and each time we do something with them, the students seem to grasp the concepts quite well. When doing the AA task, I encouraged my students to use patty paper as a tool for doing transformations. Also, this task was their first introduction to dilations.
I started by drawing 2 equiangular triangles on the board (see picture below) and asked the students if the 2 triangles were similar. A lot of them said NO because there wasn't a "nice" number to multiply 3 by to get 8. :) So, I wrote the equations from the picture and we came to the agreement that 8/3 or 3/8 would have done the trick, depending on which way we were scaling/dilating. They seemed to find this pretty magical...this should be an indication of the level of number sense my students are working with. :)
So, as they worked on the AA task, they did great with the translating and rotating. I wrote up a list of requirements (see picture below) and they were able to articulate them quite well.
They did great with the "vagueness" that I had been struggling with. So, when it came to dilating Triangle ABC (I didn't worry too much about the prime notation for this task), they knew that they had to make it bigger, but they didn't necessarily know by how much. This is where I wrote the new equation from the picture below (AB x ? = DE) and they were actually able to connect it back to the 3 and 8 sided triangles. The magic (or madness for some of them) continued. Ultimately, they were able to say that you needed to multiply it by DE/AB in order to dilate the smaller triangle to the larger triangle, and I was pleasantly surprised.
Another issue that I'm having is, Where do I go from here? I guess I'm still having difficulty wrapping my head around the fact that THIS is the new definition of similarity, but I'm getting there. Pulling it all together and not seeing these tasks as individual exercises is something that I'm still working on. I appreciate your feedback. Please forgive my vagueness or lack of precision in notation, but I think that mostly comes from trying to meet my students where they are, and let's be honest...where I am, too.
Thanks for reading!
Friday, December 13, 2013
Asilomar Mathematical Modeling Presentation
This past weekend I had the pleasure of attending the annual CMC North, Asilomar Math Conference. I have attended this conference before, but this was the first year that I was going to be a presenter at the conference. The title of my presentation was "Embedding Authentic Modeling Problems in MS/HS Curriculum" and we featured two of Dan Meyer's 3-Act Video problems (http://blog.mrmeyer.com). The audience had a choice to work on one of the two problems that we included and it seemed to go very well. I've included the presentation below. Please enjoy!
Re-Engagment Lesson
This lesson actually took place at the beginning of the year, but I am just getting around to it now...
The directions for the third page, “Between vs. Midpoint”, were to first read the student explanation, and secondly write a question or a comment that could make the argument better.
Finally, students worked on a page
of sample work called, “Angle Bisectors”, which asked them to a. look at the
student work and make sense of it, b. if the work was correct, state why, and c.
if the work was not correct, determine where the student made their mistake and
explain why it’s incorrect.
As you can see, what was required of each student was a little different from page to page. I did not want them to do the same thing for all, partly because the four pages dealt with four different mathematical ideas that I wanted to showcase. My purpose was for them to become re-introduced to the problems from the test, and to use a critical eye to determine how they might make each piece of work better if it was incorrect, or expand their knowledge if it was an unfamiliar approach.
Through
the last eight years that I have been a classroom teacher, one common thread
that stands out to me is the amount of professional development that I have
participated in. I have learned about
everything from strategies to engage English Language Learners, to how to
incorporate technology into my classroom, to how to mentor a first-year beginning
teacher. With all of the different
themes and directions that my professional growth has taken on, none of them
have been as meaningful to me as those centered on Common Core and the
Standards for Mathematical Practices.
When I was asked to participate in
the CPEC grant, I honestly had no idea what to expect, nor did I really know
anyone who was involved. I was anxious
and excited and could not wait to see what was happening in my region with
regards to Common Core. The impact that
this two-year grant has had on my teaching practice is invaluable and perhaps
even immeasurable. I continue to take
risks and try new things in my classroom, as well as persevere when I am not
successful the first or second, or even third time. One of my favorite risks that I have taken
recently was a re-engagement lesson in my Geometry classes.
I have found in my eight years of
teaching that the first chapter test is often the hardest for students. I’m not sure if this has more to do with
brushing off the dust from summer vacation, or the fact that Geometry is quite
different than Algebra. Nevertheless, my
current Geometry students played into my theory and were not overly successful
on their Chapter One test. There were
errors in notation, reasoning, and even setting up a correct equation to model
a Geometric principle; all of which are areas that need to be addressed and
remedied in order for a student to be successful in later chapters.
After grading the Chapter One tests,
it was obvious that I was faced with the age-old problem of the “haves” and the
“have-nots” in the sense that some students "have" the understanding and others don't. There was a large
population of students who were struggling with basic concepts on the test, but
there was a considerable amount of them who were successful and were ready to
move on to new applications and ideas.
So, as their teacher, what do I do?
Do I move on and hope that the “have-nots” will catch on
eventually? Or do I start over and cause
boredom and frustration amongst the “haves”?
My solution was to try a re-engagement lesson.
I chose four areas/questions that I
wanted my students to focus on. The
first three questions on the test related to Geometric notation and basic
concepts such as where two planes intersect (many said a point). The second area of concern for me was on an
error-analysis question. The majority of
students were able to articulate which student in the scenario was correct
and/or incorrect, however their explanations and justifications were weak and
unconvincing. The third and forth questions
that I chose for my re-engagement both had Algebraic applications that stemmed
from Geometry. First, an Angle
Addition Postulate problem that involved four adjacent angles (two of which
were congruent) that formed a straight angle, and asked to find the value of
the variable. Second, an angle
bisector scenario where students were given the measure of one of the smaller
angles and the larger angle, both in the forms of an Algebraic expression, and
asked to find the measure of the smaller angle.
My current class schedule is laid
out such that I teach three, 90-minute periods of Geometry every day. Every other day I see the same group of
students, so I see six periods over the span of two days. The way that this particular test panned out
was that I graded my first three classes during the first night and then graded
my second set the next night. However,
once I graded the first set of tests, I was familiar with common errors and
misconceptions, so I did not grade my second set of tests right away. Instead, I went to the photocopy machine and
made copies of student work from the second set of tests. This allowed me to copy student work that was
ungraded, so the students were unaware of the accuracy of the responses. I selected student work that represented the
common errors as well as a few correct solutions, some using a non-traditional
approach.
The next time that I saw each group
of students, this was also the day after their test, I told them that they
would get their tests back at the end of the period, but they had some work to
do first. I knew that if they received
their tests first, they would not buy in to the re-engagement activity. On the white board I had written prompts that
corresponded with each page of student work – there were four pages in total.
For the first page, titled “Notation”, students were asked to find the error in each student’s notation and make appropriate corrections. Because I photocopied the first three questions from the test and used that for each anonymous student representative, there were some pieces of each student work that were possibly correct. If that was the case, students did not need to comment.
For the first page, titled “Notation”, students were asked to find the error in each student’s notation and make appropriate corrections. Because I photocopied the first three questions from the test and used that for each anonymous student representative, there were some pieces of each student work that were possibly correct. If that was the case, students did not need to comment.
The second page was called “True
Statements About Angles” and required students to a. make sense of the student
work sample, b. determine if the work was correct, c. if the student was
correct, they needed to describe the approach, and d. if the work was
incorrect, explain why.
The directions for the third page, “Between vs. Midpoint”, were to first read the student explanation, and secondly write a question or a comment that could make the argument better.
As you can see, what was required of each student was a little different from page to page. I did not want them to do the same thing for all, partly because the four pages dealt with four different mathematical ideas that I wanted to showcase. My purpose was for them to become re-introduced to the problems from the test, and to use a critical eye to determine how they might make each piece of work better if it was incorrect, or expand their knowledge if it was an unfamiliar approach.
As students began to engage in this
activity, I was blown away by their interest and motivation to make sense of
the mathematics. Without asking them to
do so, they started taking out their notes to use as a reference, they were
communicating with their partner to see what they thought, and there were very
few questions of me. This was the polar
opposite of what I normally see in my classroom. It is a struggle for me to get them to
interact with their notes and textbook, they usually turn right to me for the
answers, and they don’t rely on their peers as resources or experts.
As I observed my students working, I
heard them discussing why a particular answer was true or false, they were
critiquing the arguments that had been provided by the selected students, and
they were working together to draw a conclusion. I even heard comments like, “I’m going to be
much more careful on my next test so that Ms. Balli doesn’t have to grade all
of this crap!” or “Oh no, I don’t think this is my work, but I know that this
is the way I did this problem, and now I see that it’s wrong.”
There was one student work sample
that I included because it was an example of an equation that had been set up
incorrectly, but yielded the correct answer.
This was an interesting discussion starter because students asked me,
“Would they get full credit? They got
the right answer!” Eventually students
began to realize that the importance did not rest in the correct answer, but
rather the correct method. It was
obvious that, to them, math is all about getting the correct answer, but they
were able to slowly move away from this because they saw evidence of getting
the right answer through an invalid process.
I believe that this was the start of a cultural shift in my classroom –
as their teacher, a correct answer is nice, but that is certainly not the only
thing that I am looking for.
When it came time to return the
tests, I did a short debrief with them about the whole re-engagement
experience. Several students stated that
they had never done anything like this before, and found it very useful. The majority of my students said that they
learned something from this lesson, and whether they scored an A or an F on the
first chapter test, they felt strongly about these particular problems that they
had examined and felt that they understood them better. Regardless of his or her grade on the test, I
did feel that each student was able to walk away from this experience with a
deeper understanding of the mathematics.
Just before handing back the tests,
I shared with my students some of the research that has been done with
relationship to feedback. The three
categories that were examined in this research study were teachers providing
only a grade (no feedback), teachers providing both written feedback and a
grade, and teachers providing only feedback (no grade). The results showed that the greatest amount
of student learning was from the population of students who only received
feedback, no formal grade. I had a good
laugh with my students, because despite the findings from this research, I had
provided them with both a formal grade and feedback. I did this because I knew that I wanted to
have my students participate in a re-engagement lesson prior to getting their
tests back, so I felt that this would be a vehicle for student learning,
regardless of me providing them with a grade.
As the research predicted, once
students received their tests with both written feedback and a formal grade,
they appeared to be ready to move on to the next topic of discussion, as there
was little interest in examining their mistakes. However, I will say that they were able to
connect mistakes that they made to mistakes that they saw from the student work
samples. The work samples may not have
been a photocopy of their work, but the same mistake was made, and I do feel
that there was something learned from making this connection.
An observation that I made about my
six Geometry classes was that, in some instances, there was not as much buy-in
from my B-Day students (second day). My
B-Day classes have fewer Honors students, as the Honors classes (English,
History, and Science) are offered more on B-Days, so I do find more Honors
students in my A-Day classes. However, I
am not sure that the schedule of classes is the only culprit. When I made photocopies of student work, I
only made copies from my B-Day classes, so I am wondering if they felt
discouraged because they recognized some of their work. Are the students in these classes not as
confident? I am not sure what the
reasoning is for the lack of connection, but I am interested to see that if I
include work from both days, would there be an increase in buy-in?
Finally, I want to take a moment to
reflect on the two successful re-engagement lessons that I have undertaken. The first re-engagement lesson that I taught
successfully was using a MARS task that I had given my students as a formative
assessment. I was teaching a unit on
surface area and volume and wanted to see how much they were able to apply to a
composite three-dimensional figure. The
task involved finding the volume of a wine-shaped glass that was part cylinder,
part hemisphere. Students struggled with
the composition of volume; forgetting to divide the volume of the sphere by
two, or did not remember the four-thirds from the sphere formula. There was a wide range of issues.
When I did the re-engagement lesson,
I provided students with six samples of student work, which they were asked to
make sense of and then determine which student had the correct answer. Without exception, every student in my three
different classes was able to articulate why “Student B” was correct. It was an amazing sight to see and I was
confident that my students had really made a connection to the mathematics from
the task.
Fast-forward a week and I am now giving them their summative
assessment. The end of unit test
included a problem asking them to find the volume of a hemisphere, and I was
devastated to find that less than a quarter of my students were successful with
this task. This made me question the
impact of the re-engagement lesson. Was
it not all that it was cracked up to be?
Was it really that effective? Or
in that moment during the re-engagement lesson did they actually connect to the
mathematics and were unable to make the connection to this new problem? Is the issue in their ability to see how
these concepts work together?
I am finding that this year I am eager to assess my students,
simply so that I can take them through the process of re-engagement. I am also excited to explore the applications
of re-engagement outside of assessment, as well as outside of mathematics. Would a re-engagement lesson be applicable or
effective in Science or Spanish? What
about English or History? As I gain
confidence in my teaching, I am open to sharing my thoughts and experiences
with others, because I know that there are so many things that I have yet to
learn. Not only have I learned from
professional development seminars, which are lead and populated by adults, but
even more so I have learned from the people that are inside the walls of my
classroom everyday; my students.
Saturday, October 5, 2013
Animoto and Geometry
I always want my students to make connections between math and their surroundings, especially when it comes to Geometry. We are just now wrapping up the chapter on parallel lines cut by transversals, and I think there are so many examples of some of the Geometric ideas that we cover in their everyday environment. So, I had them download the free app Animoto and it was great because more than half of each class had the capacity to do so, which made groups small and doable.
I had students get into groups of two and walk around campus looking for various Geometric elements. I had a list of twelve, which they had to find a minimum of ten. The list included:
Overall, I found that the students took the activity seriously. They loved being outside and making connections to what they were learning in class. They still relied on me for things like, "Mrs. Murk, would this be an example of Parallel Planes?" They still struggle with self-starting, but for the most part, they took the initiative.
Something that I would change for next time is I would be stricter, or more descriptive, as to what the pictures are of. I don't want students to find two lines that are intersected by a transversal and use that picture for three or four different Geometric idea. I just find this boring and not pushing the students very hard to be creative.
I've included some of my favorite videos below.
Geometry shtuff
Thomas and Ben's swag master geometry video
My Video
I had students get into groups of two and walk around campus looking for various Geometric elements. I had a list of twelve, which they had to find a minimum of ten. The list included:
- Parallel Lines
- Perpendicular Lines
- Alternate Interior Angles
- Alternate Exterior Angles
- Same-Side Interior Angles
- Corresponding Angles
- Intersecting Planes
- Supplementary Angles
- Complementary Angles
- Vertical Angles
- Parallel Planes
- Skew Lines/Segments
Overall, I found that the students took the activity seriously. They loved being outside and making connections to what they were learning in class. They still relied on me for things like, "Mrs. Murk, would this be an example of Parallel Planes?" They still struggle with self-starting, but for the most part, they took the initiative.
Something that I would change for next time is I would be stricter, or more descriptive, as to what the pictures are of. I don't want students to find two lines that are intersected by a transversal and use that picture for three or four different Geometric idea. I just find this boring and not pushing the students very hard to be creative.
I've included some of my favorite videos below.
Geometry shtuff
Thomas and Ben's swag master geometry video
My Video
Subscribe to:
Posts (Atom)