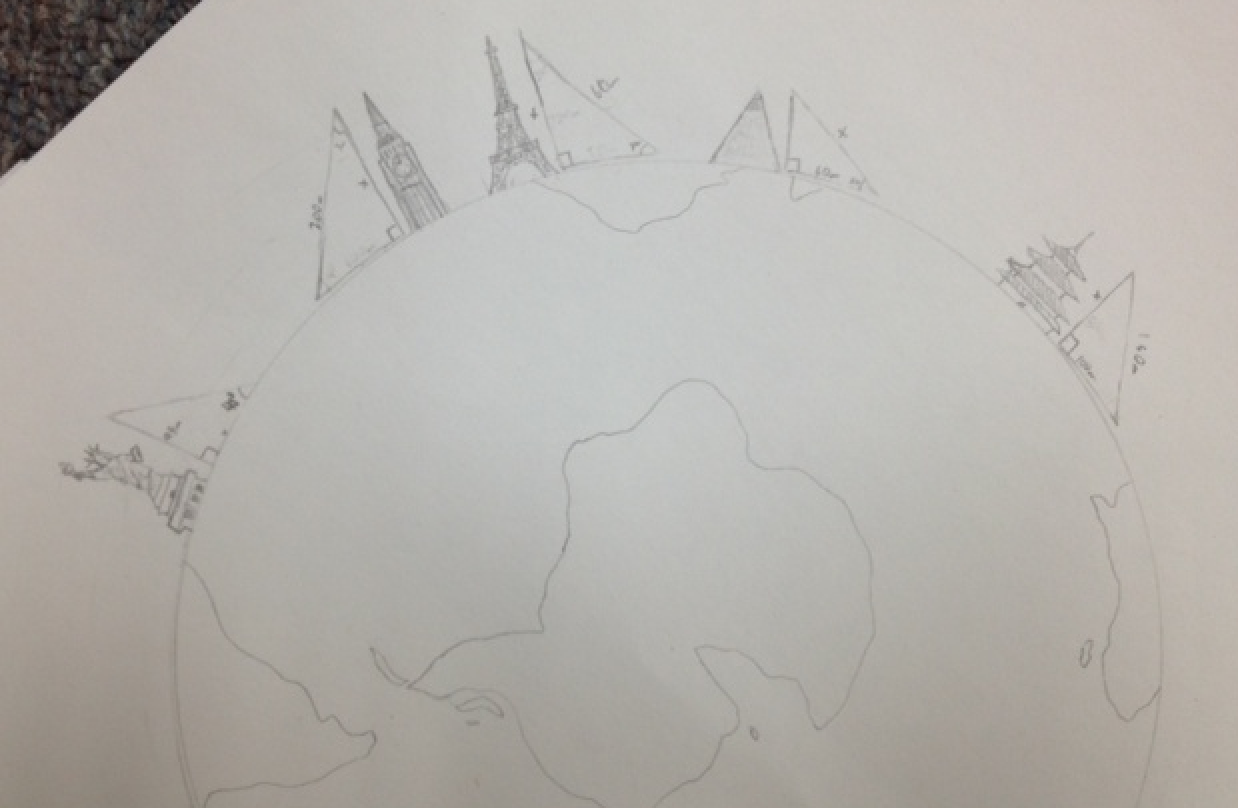
So, as I mentioned in a previous post, I've had my students build their own trig-tables this year and I must say that they are doing extremely well! I was inspired by my amazing colleague, Amy Zimmer (http://zicker63.blogspot.com) to do this fun activity with my students. The original document involved a scene set in a park (see below, original document found at: http://www.funmaths.com/worksheets/downloads/view.htm?ws0012_1.gif) and Amy thought that it would be cool to switch it up and have the students come up with their own scene. In the woods, at the beach, in the kitchen, etc.
The requirement for the assignment was that they needed to create some sort of scene or scenario where they were setting up right triangles that they could solve for missing sides and angles. Another requirement was that they needed to set up one problem that involved using the ratio altitude/base, one using altitude/hypotenuse, and one using base/hypotenuse, all given one acute angle and one of the side lengths in the ratio. The fourth type of triangle they had to set up should have had both acute angles missing and given two side lengths, basically using inverse trig. The fifth triangle did not have a requirement, they could repeat any of the other types of triangles (the wildcard).
I enjoyed seeing their work and seeing how creative they got. The creation of the poster was essentially phase one of the activity and phase two was actually solving for all missing values of the triangle. Students jumped right in to using their trig charts and did surprisingly well with the triangles that were missing their acute angles. I really enjoyed seeing them do this because I think even high school students need to show their inner artist and get a little crafty sometimes. I had them staple their work to the back of the poster and any student that worked on the poster had to submit a page of work. I've included some of my favorites. Thanks, Amy for the inspiration! Enjoy!
From Amy Zimmer's Class:
Tuesday, April 15, 2014
Tuesday, April 8, 2014
Building Trig Tables
I'm sure I'm not the only Geometry teacher out there who gets frustrated with how their textbook approaches a subject. Right Triangle Trigonometry, for me, is one of those subjects. The textbook that my school uses just dives right in to introducing sine, cosine, and tangent with little to no context, and certainly no mention of similar right triangles. So, this year, I decided to do things a little differently.
A few months ago I was doing some work with the incredible Kate Nowak and this exact topic came up. She shared with us that when she was a classroom teacher, she had her students build their own trig tables and she ended the lesson with a Romeo & Juliet problem where Romeo needed to find how high the balcony was so that he could climb to see his star-crossed lover. (Check out Kate's blog post: http://function-of-time.blogspot.com/2009/04/introducing-right-triangle-trig.html) I thought I would give it a shot with my students.
I am teaching 6 sections of Geometry this year, so I thought that this would be a great opportunity to collect lots of data to calculate some reasonable values for sine, cosine, and tangent, even though they would not be called that until later.
Much like Kate's blog suggests, I had my students start by drawing 5 right triangles with a specified acute angle on an 8.5 by 11 piece of printer paper. This was challenging for some because a lot of my students do not know how to operate a protractor. Once we got over that hurdle, they were on their way.
After drawing their 5 right triangles, I set them up to measure the three side lengths of each triangle, using Kate's handout, students recorded their measurements. The third step was to calculate the ratios of the side lengths (aka: sine, cosine, tangent) :) of their 5 triangles. Lightbulbs began to go on around the room because students were realizing that their ratios for the 5 different triangles were all the same (or at least pretty close). This was a great opportunity to take a look at some data and discuss potential outliers or mistakes. Here's a sample of student data:
What I found was that students were not yet ready to be the "critical consumers" that I was wanting them to be. This sample doesn't have any glaring errors, but nevertheless, they were willing to accept the data at face value. I asked them to look for patterns and initially I was hearing things like "It's going up by 0.3". Well, that may be true for the "altitude" column from row 1 to row 2, but they didn't know how to look for any other type of pattern. Finally someone said, "They're all increasing," which was wonderful to hear! We talked about why that was a good sign and why it made sense. Then another student pointed out that the hypotenuse values were always the largest in the set of 3 data points and we discussed why that was a good thing. Next, we practiced finding the ratios to make sure that they were dividing correctly. It was great to discuss why all the numbers should be less than 1 or why a number should be bigger than another; conversations that I don't think they had ever had. Lastly, we practiced finding the averages of the 5 different ratio entries. I have to say, this was a bit of a train wreck! For example, in the first column (a/b), students told me that the average was 1.4 or something like that. They didn't understand why that was not possible. After some discussion, they were convinced that the average needed to be closer to 0.2-something.
Because I have so many sections of Geometry and so many students in each section, I thought this would be a great opportunity to collect lots of data, but also calculate averages. Each student was working with a specific acute angle, but so was their partner, so once they got their ratio averages, I had them average their averages with their neighbor. That's what we wrote in the yellow charts on the board (see below).
The last step in this process was to look at all this data and determine if the numbers were reasonable from all 6 classes. I told the students that if they were comfortable with all the entries, they should calculate the average, if they felt that there was an outlier (or more than one), they should be able to defend why, throw it out, and then find the average of the remaining numbers. This was an interesting process because some students argued to keep specific numbers while others fought to get rid of them. The final product for each class was their own trig table (see below), which was a lot of work, but now we were ready to do some trig! :)
So, now it was time to actually do some work and I had a moment of panic (I actually lost some sleep over this) because I wasn't sure how I was going to bring this all together. Kate's worksheet had some great questions, so I started there. First of all, I wanted to take some time to marvel at the fact that all of this data collection happened independently (no two classes worked together), so how was it that their data was so close? To my surprise, it seemed that students had already considered this and very quickly responded with "Because the triangles are similar!" We discussed this further and it was clear that they understood the idea of similar triangles by AA. I felt they were ready to put this stuff to good use.
The last problem on Kate's handout involved Romeo & Juliet, and I thought we could give it a shot. I tried a sample using a 30 degree angle and a base of 50 feet. I asked students what I was solving for, they knew it was altitude, and then I asked, do I know anything about the relationship between altitude and base of a right triangle with a 30 degree angle? And that's when the lightbulbs REALLY started to go on! What an amazing moment for the students to realize that all of their hard work had lead them to this place where they could solve a problem without me telling them what to do. They were off to the races and solving for all different angles.
The last thing that I did was said, "Now, Romeo really wants to impress Juliet, so he is fashioning a zip-line for her to ride down and meet him. If he is 70 feet away, how long with the line need to be for your given angle?" Some started to set up the same ratio as before, but quickly realized that this relationship was now base and hypotenuse. After realizing that, they were able to set up the correct equation, but I have to say, solving it proved to be a bit more difficult. :)
Even though I spent a whole week doing this with my students (3 periods on block schedule), I feel that it was totally worth the time and effort that the students put in. They worked with data, they were critical, precise, and thoughtful, which are things that don't usually happen for them in a math classroom. Overall, I feel that this was a huge success, but I am already waiting for them to get mad at me when I tell them that they can just use a calculator to do some of this stuff. :)
A few months ago I was doing some work with the incredible Kate Nowak and this exact topic came up. She shared with us that when she was a classroom teacher, she had her students build their own trig tables and she ended the lesson with a Romeo & Juliet problem where Romeo needed to find how high the balcony was so that he could climb to see his star-crossed lover. (Check out Kate's blog post: http://function-of-time.blogspot.com/2009/04/introducing-right-triangle-trig.html) I thought I would give it a shot with my students.
I am teaching 6 sections of Geometry this year, so I thought that this would be a great opportunity to collect lots of data to calculate some reasonable values for sine, cosine, and tangent, even though they would not be called that until later.
Much like Kate's blog suggests, I had my students start by drawing 5 right triangles with a specified acute angle on an 8.5 by 11 piece of printer paper. This was challenging for some because a lot of my students do not know how to operate a protractor. Once we got over that hurdle, they were on their way.
After drawing their 5 right triangles, I set them up to measure the three side lengths of each triangle, using Kate's handout, students recorded their measurements. The third step was to calculate the ratios of the side lengths (aka: sine, cosine, tangent) :) of their 5 triangles. Lightbulbs began to go on around the room because students were realizing that their ratios for the 5 different triangles were all the same (or at least pretty close). This was a great opportunity to take a look at some data and discuss potential outliers or mistakes. Here's a sample of student data:
Because I have so many sections of Geometry and so many students in each section, I thought this would be a great opportunity to collect lots of data, but also calculate averages. Each student was working with a specific acute angle, but so was their partner, so once they got their ratio averages, I had them average their averages with their neighbor. That's what we wrote in the yellow charts on the board (see below).
Each class generated this chart and now it was time to compare the charts from the 6 different classes. I asked students to help me calculate averages from the yellow chart (if there was more than one entry) as well as help me understand if any of the numbers just did not make sense. They picked up on things like increasing and decreasing patterns, and if there were two entries in a cell they were able to compare two numbers and see if they were reasonable or not. The next step involved me writing up the numbers from each class into a fairly large chart on the white board (see below).
So, now it was time to actually do some work and I had a moment of panic (I actually lost some sleep over this) because I wasn't sure how I was going to bring this all together. Kate's worksheet had some great questions, so I started there. First of all, I wanted to take some time to marvel at the fact that all of this data collection happened independently (no two classes worked together), so how was it that their data was so close? To my surprise, it seemed that students had already considered this and very quickly responded with "Because the triangles are similar!" We discussed this further and it was clear that they understood the idea of similar triangles by AA. I felt they were ready to put this stuff to good use.
The last problem on Kate's handout involved Romeo & Juliet, and I thought we could give it a shot. I tried a sample using a 30 degree angle and a base of 50 feet. I asked students what I was solving for, they knew it was altitude, and then I asked, do I know anything about the relationship between altitude and base of a right triangle with a 30 degree angle? And that's when the lightbulbs REALLY started to go on! What an amazing moment for the students to realize that all of their hard work had lead them to this place where they could solve a problem without me telling them what to do. They were off to the races and solving for all different angles.
The last thing that I did was said, "Now, Romeo really wants to impress Juliet, so he is fashioning a zip-line for her to ride down and meet him. If he is 70 feet away, how long with the line need to be for your given angle?" Some started to set up the same ratio as before, but quickly realized that this relationship was now base and hypotenuse. After realizing that, they were able to set up the correct equation, but I have to say, solving it proved to be a bit more difficult. :)
Even though I spent a whole week doing this with my students (3 periods on block schedule), I feel that it was totally worth the time and effort that the students put in. They worked with data, they were critical, precise, and thoughtful, which are things that don't usually happen for them in a math classroom. Overall, I feel that this was a huge success, but I am already waiting for them to get mad at me when I tell them that they can just use a calculator to do some of this stuff. :)
Subscribe to:
Posts (Atom)